Прогноз на досрок по информатике ЕГЭ 2023 (задания и ответы)
ЕГЭ 2023. Экзаменационная работа состоит из 27 заданий с кратким ответом, выполняемых с помощью компьютера.
На выполнение экзаменационной работы по информатике отводится 3 часа 55 минут (235 минут).
В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.
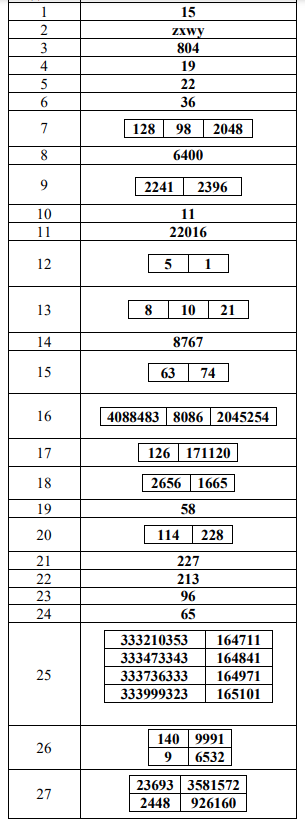
1. На рисунке схема дорог N-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта А в пункт Б и из пункта Д в пункт Е. В ответе запишите целое число.
На выполнение экзаменационной работы по информатике отводится 3 часа 55 минут (235 минут).
В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.
1. На рисунке схема дорог N-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта А в пункт Б и из пункта Д в пункт Е. В ответе запишите целое число.
2. Логическая функция F задаётся выражением ¬(x → w) ∨ (y ≡ z) ∨ y На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3. В файле приведён фрагмент базы данных «Кондитерские изделия» о поставках конфет и печенья в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой половины августа 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт внесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид. Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
4. По каналу связи передаются сообщения, содержащие только буквы из набора: В, Д, К, Н, О, Р. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 0, К – 1001. Для четырёх оставшихся букв В, Д, О и Р кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КОНОВОД, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
5. На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. Далее эта запись обрабатывается по следующему правилу: а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10; б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11. Полученная таким образом запись является двоичной записью искомого числа R. Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, не меньшее 60. В ответе запишите это число в десятичной системе счисления.
6. Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n – целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Повтори 2 [Вперёд 7 Направо 90 Вперёд 18 Направо 90] Поднять хвост Назад -2 Направо 90 Вперёд 9 Налево 90 Опустить хвост Повтори 2 [Вперёд 8 Направо 90 Вперёд 5 Направо 90] Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на линиях.
7. Для хранения произвольного растрового изображения размером 1024 на 120 пикселей отведено 210 Кбайт памяти без учёта размера заголовка файла. При кодировании каждого пикселя используется 7 бит для определения степени прозрачности и одинаковое количество бит для указания его цвета. Коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов (без учёта степени прозрачности) можно использовать в изображении?
Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
Для хранения сжатого произвольного растрового изображения размером 640 на 256 пикселей отведено 170 Кбайт памяти без учёта размера заголовка файла. Файл оригинального изображения больше сжатого на 35%. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
Для хранения сжатого произвольного растрового изображения размером 640 на 256 пикселей отведено 170 Кбайт памяти без учёта размера заголовка файла. Файл оригинального изображения больше сжатого на 35%. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
8. Определите количество пятизначных чисел, записанных в девятеричной системе счисления, в записи которых ровно одна цифра 3, при этом никакая из цифр 5, 6, 7, 8 не стоит рядом с цифрой 3.
9. Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: – в строке только одно число повторяется ровно два раза, остальные числа различны; – среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел. В ответе запишите только число.
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: – наибольшее из четырёх чисел меньше суммы трёх других; – четыре числа нельзя разбить на две пары чисел с равными суммами. В ответе запишите только число.
9. Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: – в строке только одно число повторяется ровно два раза, остальные числа различны; – среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел. В ответе запишите только число.
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: – наибольшее из четырёх чисел меньше суммы трёх других; – четыре числа нельзя разбить на две пары чисел с равными суммами. В ответе запишите только число.
10. Текст романа М.А. Булгакова «Собачье сердце» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречаются в тексте слова с сочетанием букв «куда», например «откуда», «кудахтать». Отдельные слова «куда» и «Куда» учитывать не следует. В ответе запишите только число.
11. При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.
12. Исполнитель Редактор получает на вход строку символов и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
13. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л. Для каждой дороги указана её длина. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого короткого пути из города А в город М? На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого длинного пути из города А в город М? Длиной пути считать количество дорог, составляющих этот путь.
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
11. При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.
12. Исполнитель Редактор получает на вход строку символов и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
13. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л. Для каждой дороги указана её длина. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого короткого пути из города А в город М? На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого длинного пути из города А в город М? Длиной пути считать количество дорог, составляющих этот путь.
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
14. Операнды арифметического выражения записаны в системе счисления с основанием 15. 123×515 + 1×23315 В записи чисел переменной x обозначена неизвестная цифра из алфавита 15- ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
15. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m»; и пусть на числовой прямой дан отрезок B = [50; 70]. Для какого наибольшего натурального числа А формула ДЕЛ(x, A) ∨ ((x ∈ B) → ¬ДЕЛ(x, 21)) тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х? ИЛИ Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) \/ (x + A ≥ 80) тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х?
15. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m»; и пусть на числовой прямой дан отрезок B = [50; 70]. Для какого наибольшего натурального числа А формула ДЕЛ(x, A) ∨ ((x ∈ B) → ¬ДЕЛ(x, 21)) тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х? ИЛИ Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) \/ (x + A ≥ 80) тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х?
16. Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n × F(n − 2), если n > 1. Чему равно значение выражения F(2023) / F(2019)?
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n + F(n − 1), если n > 1. Чему равно значение выражения F(2023) — F(2019)?
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = n при n <= 2; F(n) = n + F(n − 2), если n > 2. Чему равно значение выражения F(2023) + F(2020)?
17. В файле содержится последовательность натуральных чисел. Элементы последовательности могут принимать целые значения от 1 до 100 000 включительно. Определите количество пар последовательности, в которых хотя бы одно число делится на минимальный элемент последовательности, кратный 21. Гарантируется, что такой элемент в последовательности есть. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности
18. Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n + F(n − 1), если n > 1. Чему равно значение выражения F(2023) — F(2019)?
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = n при n <= 2; F(n) = n + F(n − 2), если n > 2. Чему равно значение выражения F(2023) + F(2020)?
17. В файле содержится последовательность натуральных чисел. Элементы последовательности могут принимать целые значения от 1 до 100 000 включительно. Определите количество пар последовательности, в которых хотя бы одно число делится на минимальный элемент последовательности, кратный 21. Гарантируется, что такой элемент в последовательности есть. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности
18. Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Похожие публикации
Изменения в КИМ ОГЭ 2024 года по сравнению с 2023 годом
Русский язык В целом структура и содержания экзаменационной модели КИМ не претерпели существенной трансформации. ИзмененияВ данной публикации отсутствуют комментарии !
Перед публикацией, советую ознакомится с правилами!
Комментарии
Официальная диагностическая работа МЦКО по русскому языку 8 класс (задания и ответы)
Здравствуйте. Ссылка работает, материалы доступны для скачивания
Отзывы и предложения по сайту my-exam.com
Здравствуйте! Все новые варианты загружены на тот же гугл диск. Если у вас возникнут сложности, то
Официальная диагностическая работа МЦКО по русскому языку 8 класс (задания и ответы)
Ссылка не работает
Отзывы и предложения по сайту my-exam.com
Добрый день , Спасибо за ВПР 4 класс , очень помогли. Но у меня вопрос 03,12.24 оплачивала
Отзывы и предложения по сайту my-exam.com
Здравствуйте! Все ВПР составлены в соответствии с демоверсиями ВПР 2025 года. Более того, сейчас
Все комментарии на сайте..